
Explanation:
We learned that the
periodogram is an asymptotically unbiased but inconsistent
estimator for the PSD. For a stationary random process, the
averaged periodogram approach (also called the Bartlett's
method) is a simple but effective way to estimate its PSD.
The algorithm works like this: given a single record of N data,
break the data record into K sub-records of length
L each so that N=K*L. Calculate the
periodogram for each of the K sub-records and then
average them to obtain the averaged periodogram.
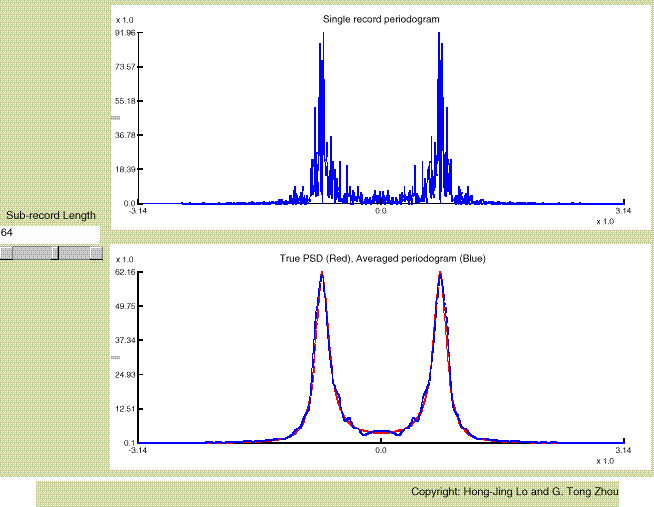
Since each sub-record has less amount of data, resolution in the averaged periodogram is lower and the bias is greater. However, averaging reduces variance of the raw periodogram and hence the averaged periodogram is less erratic. We would like to have both low bias and low variance, but for a fixed data length, K and L cannot be increased simultaneously. We therefore experience the classical bias-variance tradeoff. In general, if we know a priori that the random process x(n) has a short memory, we can choose a small sub-record length (and hence use more averaging). If on the other hand, we know that the random process is strongly correlated, then a larger sub-record length is more appropriate.
This applet assumes that N=2,048 samples of x(n) are available. The user is free to choose the sub-record length L. To experiment with the applet, first select the poles and zeros of the system. Once the system is determined, the theoretical PSD can be calculated. The periodogram of one sample realization is plotted in the top panel: it has an erratic appearance owing to the fact that the periodogram is an inconsistent estimate of the PSD. For a chosen sub-record length, the applet plots the averaged periodogram (blue) in the bottom panel together with the true PSD (red). By varying the sub-record length, the tradeoff between the bias and variance is observed.

Experiment it yourself!
Click here to run the experiment using
your browser.
Instruction: To change a parameter from its default value, slide the bar beneath the parameter window or enter a specific number and then hit the return key. Hitting the return key from any of the parameter windows initiates another Monte Carlo run.