
Explanation:
If a linear system has system function H(z)=B(z)/A(z),
then the roots of the numerator polynomial B(z) are
zeros of the system
whereas the roots of the denominator polynomial A(z) are
poles of the system. For a system with real valued impulse response,
poles and zeros must occur in conjugate symmetric pairs.
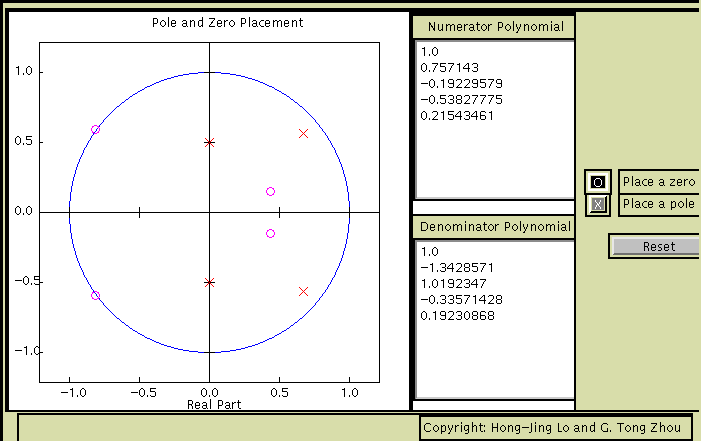
This applet generates coefficients of B(z) and A(z) , in increasing orders of 1/z, for user prescribed pole-zero locations. To place zeros, first depress the O button and then move the cursor to a desired zero location and click. O appears at the desired as well as the complex conjugated locations because we assume that the system is real valued. Similarly, to place poles, first depress the X button and then move the cursor to a desired pole location and click. Both the chosen and the conjugated positions will be marked by X. The numerator and denominator polynomial coefficients are updated every time a mouse button is clicked. In the above example, the B(z) coefficients are: [1 0.757143 -0.19229579 -0.5382775 0.21543461] which correspond to zeros with magnitudes 1 and 0.46 and phase angles at 144, -144 and 19, -19 degrees. The A(z) coefficients are: [1 -1.3428571 1.0192347 -0.33571428 0.19230868] which give poles with magnitudes 0.88 and 0.5 and phase angles at approximately 40, -40 and 90, -90 degrees.
Experiment it yourself!
Click here to run the experiment using
your browser.