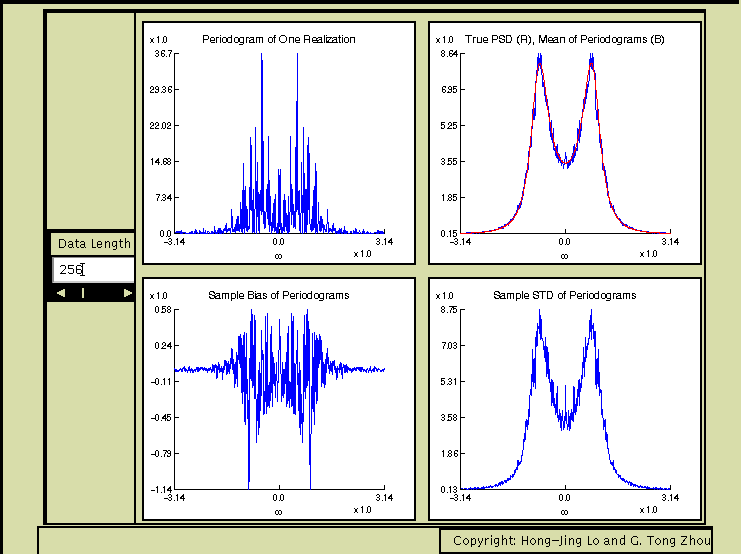

Explanation:
Let x(n) be a zero-mean, stationary random process and
denote by X(w) its discrete Fourier transform (DFT).
The periodogram of x(n) is defined as I(w)=|X(w)|^2 /N,
where N is the data length. It is known that the periodogram
is an asymptotically unbiased but inconsistent estimator for the
power spectral density (PSD) S(w). This means that
as N goes to infinity, the expected value of
I(w) goes to S(w), but the variance of
I(w) will not reduce. Interestingly, it can be shown
that the standard deviation (std) of I(w) is approximately
S(w) except at the zero frequency:
the std of I(0) is approximately
sqrt(2)*S(0). The purpose of this applet is to illustrate
these properties.
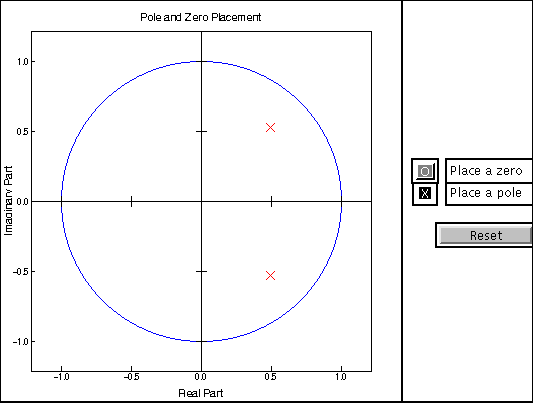
We focus our attention on linear and stationary random processes here. To use this applet, first select the poles and zeros of the system. Once the system is determined, theoretical PSD can be calculated. The periodogram from a sample realization is plotted in the top left window. It has an erratic appearance owing to the fact that the periodogram is an inconsistent estimate of the PSD. The applet then generates 200 independent realizations of x(n), computes the periodograms, and then averages all periodograms to obtain the empirical mean as shown in the top right window (blue). The true PSD (red) is displayed in the same window for comparison. Their difference - the empirical bias is shown in the bottom left window whereas the empirical std is plotted in the bottom right window. By adjusting the data length N, one can observe that the bias in the periodogram decreases with N but the std stays about the same. Moreover, the std of the periodograms resembles the true PSD except at w=0 where the two differ by about 40%.
Experiment it yourself!
Click here to run the experiment using
your browser.
Instruction: To change a parameter from its default value, slide the bar beneath the parameter window or enter a specific number and then hit the return key. Hitting the return key from any of the parameter windows initiates another Monte Carlo run.
Warning: This applet runs relatively slowly because 200 independent realizations are used.