
Explanation:
Suppose that Xi, i=1, 2, ..., n, are independent, identically
distributed random variables with mean m and
variance s^2. The sample mean (running average)
is defined as mX=(X1+X2+...+Xn)/n. It is clear that
mX is also a random variable and hence has its own
mean and variance. We can show that if s^2 is
finite, then the mean of mX equals m (we say
that mX is an unbiased estimator for m ),
and the variance of mX is s^2/n. Therefore,
if n is increased to infinity, then the variance of
mX is reduced to 0 - this is a property called
consistency. Most random variables have finite variances
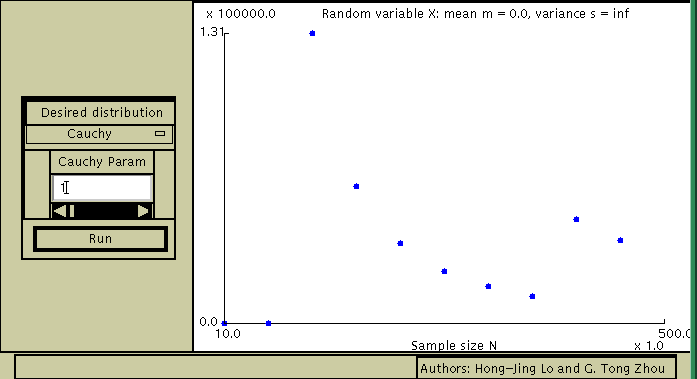
but there are exceptions - one such example is the Cauchy
r.v.
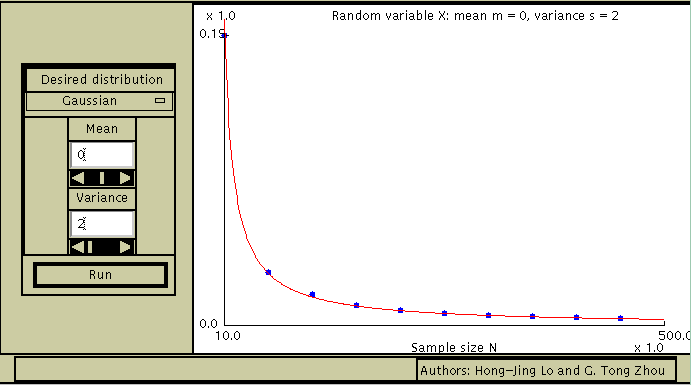
To use this applet, first select the pdf of Xi from the Desired distribution menu (default=Gaussian). Next, set the corresponding distribution parameters and click on Run . The program first displays the true mean m and variance s^2 at the top right of the applet. For a given sample size n, the program generates 500 sets of such random variables, each set containing n samples. It then computes the sample mean for each set, calculates the variance across these 500 sample mean values, and places a blue dot in the graphic window. This is done for a number of sample sizes n. The values are then compared with the red curve s^2/n which indicates the true variance of the sample mean as a function of n.
Note that the blue dots agree fairly well with the red curve when the variance s^2 of the distribution is finite. For the Cauchy distribution however, the variance of the sample mean estimator does not decrease as n is increased - the sample mean estimator is inconsistent in this case because the Cauchy r.v. has infinite variance.
Experiment it yourself!
Click here to run the experiment using
your browser.
Instruction: To change a parameter from its default value, slide the bar beneath the parameter window or enter a specific number and then hit the return key. Hitting the return key from any of the parameter windows initiates another Monte Carlo run.