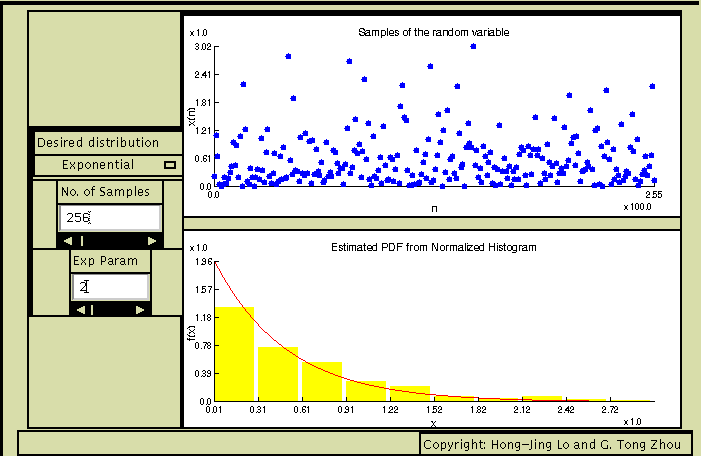

Explanation:
We encounter a number of probability distributions that possess
closed-form expressions. One way to characterize a random variable
(r.v.) is to write down its probability density function (pdf).
For example, an exponential r.v. X has pdf
f(x)=k exp(-k*x), for x>=0.
Pick the number of samples (default=256) and the exponential pdf parameter
k (default=1) from the parameter windows on the left. Once the
parameters are selected, the top right window displays, as dots, samples
of this distribution. For an exponential r.v. for example, we see that
all permissible values are in the x>=0 region, and the density
of these dots is higher as we move closer to the x=0 axis.
Histogram is a bin counter and its normalized version
can be used to estimate the pdf from the samples. The bottom
right window shows in red,
the true pdf and in yellow,
the normalized histogram. In general, the larger the sample
size, the better the ability of the normalized histogram to
approximate the true pdf.
Experiment it yourself!
Click here to run the experiment using
your browser. "Desired distribution" is a pull-down menu
which includes Gaussian, uniform, exponential, Cauchy, double
exponential, and discrete integer distributions.
To change a parameter from its default value, slide the
bar beneath the parameter window or enter a specific number and
then hit the return key. Hitting the return key from
any of the parameter windows initiates another Monte Carlo run.