
Explanation:
If r.v. X has probability density function (pdf)
f(x) and cumulative distribution function (cdf)
F(x), then we can show that a new r.v.,
U=F(X), is uniformly distributed in [0,1].
Therefore, we can generate samples of r.v. X
by first obtaining samples of U from
the uniform [0,1] distribution, and then using the inverse
of F to map U into
X. For a pdf to be "valid", it must be non-negative valued,
and has a total area of 1. Our program takes care of the second
constraint by properly scaling the pdf drawings.
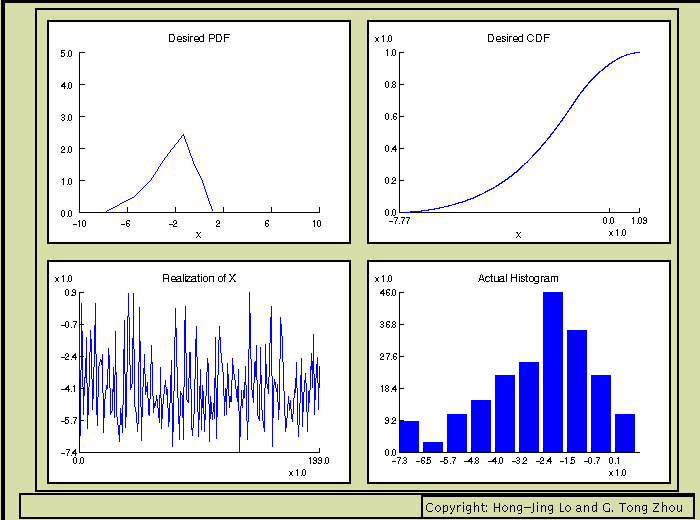
The first window that pops up is a "Work Pad" on which the user mouse-draws a pdf. The main applet window then echoes this pdf (after some smoothing and interpolation operations) in the top left window. The corresponding cdf is plotted in the top right window, and samples from this desired distribution are shown next. From the sample histogram, we can see that as the number of samples (which can be set in the Work Pad window) increases, the histogram approximates better the user defined pdf.
Experiment it yourself!
Click here to run the experiment using
your browser.